前言
本文的内容是基于递归来讲的,而回溯是递归算法的关键。总的来说这篇文章很有趣,大部分内容都跟玩游戏有关。基于上一篇《递归》来看此文没什么压力,不过还是有些重点需要记录一下。
知识点
N皇后问题
这是一个很出名的问题,给你一个8X8的国际象棋的棋盘,如何放置放置八个皇后(皇后的攻击范围是横竖线、对角线)让她们不能相互攻击?伪代码如下:
如果是4X4棋盘,可以画出递归树如下: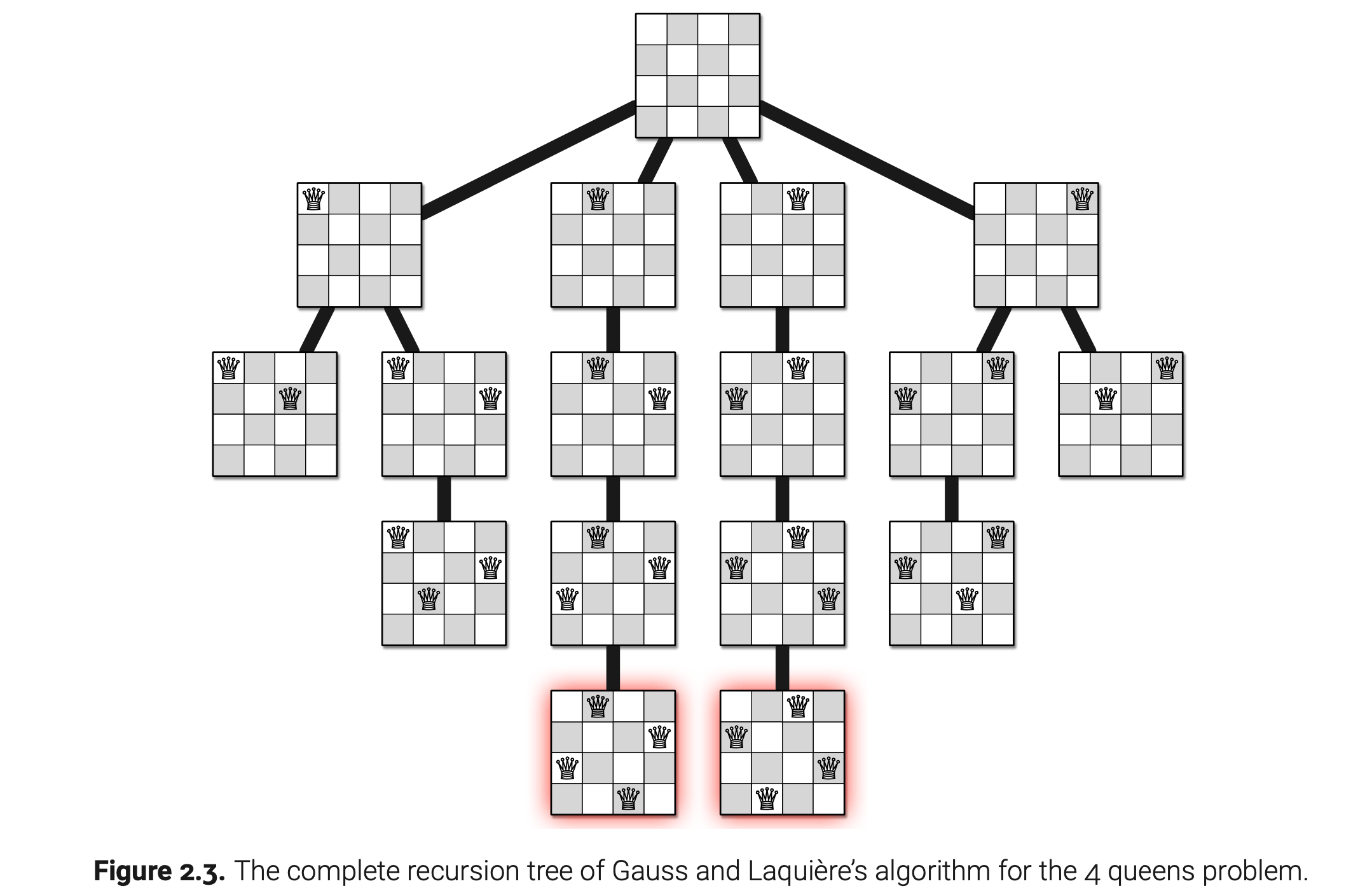
子集和
我们来看一个稍微复杂点的问题:给你一个正整数集合X和一个目标整数T,X是否存所有元素和为T的子集?比如,如果X={8,6,7,5,3,10,9}且T=15,那么符合要求的子集是存在的({8,7},{7,5,3},{6,9},{5,10})。但如果X={11,6,5,1,7,13,12}且T=15,那么答案则是不存在。
这里还有两种特殊的情况,如果T=0,答案是存在。另外,如果T<0,答案是不存在。
对于所有一般情况,对于任意x ∈ X,如果X存在所有元素和为T的子集,有以下两种情况:
•X存在一个所有元素和为T的子集,并且它包含x。
•X存在一个所有元素和为T的子集,并且它不包含x。
那么根据这个思路设计算法如下:
分析
为了方便分析这个算法,我们需要把一些细节描述的更清楚。首先,我们可以使用数组来代替集合,接着我们把原算法中“任意元素”改成“数组的最后一个元素”,那么原函数变成了(其实这里最好把数组变为全局变量,不然会增加很多内存消耗):
接下来可以的出递推式$T(n)\leq 2T(n-1)+O(1)$,那么通项公式就是$T(n)=O(2^n)$,也就是说这个算法考虑了$2^n$个X的子集。
变形
有时候我们需要具体知道这个子集有哪些元素,那么算法改造如下:
普遍的模式
回溯算法就是在做一系列决定,这些决定的目标是构造一个满足确定约束的递归定义的结构。通常这个目标结构本身就是一个序列。例如:
•在多皇后问题中,目标就是一个皇后位置的序列,每行一个,任意两个之间不能互相攻击。对于每一行算法都会决定皇后放在那个位置。
•在变形的子集和问题中,目标就是一个特定元素和的序列。对于每一个加入的元素算法都会决定它是否包含在输出序列中。
在回溯算法的每次递归调用中,都需要基于前面的决定再做出一个决定。这样我们每次要求考虑还未使用的数据,还要对前面的决定做出总结。考虑到效率问题,对于过去决定的总结应该尽量简单。例如:
•对于多皇后问题,不仅需要传入空行的数目,还需要已经放置皇后的位置。这里不太走运,我们需要完整记录过去所做的决定。
•对于子集和问题,不仅需要传入剩余元素,还需要传入剩余目标整数(原始目标整数减去过去选择的元素)。这里在过去选择了哪些元素并不重要。
在我们设计一个回溯算法的时候,我们必须考虑哪些过去决定的信息是有必要保留的。如果这信息是不平凡的,我们的递归算法也许要先解决一个更平凡的问题而不是我们被要求解决的原始问题。(这种情况类似上一章的MomSelect,先解决如何在线性时间内找到一个未排序素组的中间元素,然后得出一个算法来找到任意第k个元素)
通常一开始思考递归问题我们可以使用暴力递归,尝试所有由过去决定组成的下一个决定,不要自作聪明的去跳过一些明显很蠢的选择,尝试所有可能。等算法正确执行后再去想怎么优化。
文本分割
假设给你一段英文字母,其中没有标点符号和空格,也没有告诉你发音,你想把它分段成为由独立单词组成的句子。假设给你一个函数判断一段字符是不是单词,那么一个简单的算法设计如下(尽量不要把数组作为入参,这样执行起来会很慢,这里我们把数组当做全局变量存下来):
分析
对于大多数回溯算法有着指数级的运行时我们不应该感到惊讶。要分析此类算法精确的运行时需要一些超出本书范围的技术。幸运的是我们在本书范围讲的回溯算法只是一些更有效算法的中间媒介,这就表示它的确切运行时并不重要。
我们来分析Splittable算法的运行时。因为不知道IsWord的耗时,所以我们这里只计算它的调用次数。下面可以看到一个糟糕的递推式
不过如果你看破这里的玄机就不一样了。
首先,我们要用一个明确的表达式αn来代替O(n),α是一个未知常数。接着,我们假设算法执行了所有可能的递归调用。然后我们有如下代数变换:
最后在简化变成$T(n)=2T(n-1)+α$,这就表示$T(n)=O(2^n)$。
此外,这个分析也是严谨的。这里确实有$2^{n-1}$种分割方法—每一个输入的字符都有可能是一个单词的结尾或者不是。极端情况下,Splittable算法有必要探索这$2^{n-1}$种可能性。
变形
上面的分割方法太过于简单粗暴了,并不是人人都会满意。如果一个字符串不止一种分割方法,我们也许想要根据某种标准找到一个最佳分割;相反的,如果一个字符串不能分割成一个句子,我们也会想找到一种最能被接受的分割,而不仅仅是返回一个失败。为了达成这两个目标,假设我们可以使用一个函数Score,它可以接收一个字符串并返回一个数值。比如,我们会给更长更通用的单词打高分,给更短更复杂的单词打低分,给一些拼写错误打一点负分,给一些明显不是单词打更低的负分。我们的目标是找到一个分数最高的分割。
对于任意索引i,使用函数MaxScore(i)来计算字符串A[i..n]的最高分。那么这个函数满足一下递推式:
这个递推式和Splittable是一样的,唯一的却别就是布尔运算符∨和∧变成了数值运算符max和+。
最长递增子序列
对于任意序列S,子序列就是从S中删除零个或者多个元素剩下的序列,并且保持顺序不变;子序列中的元素并不要求在S中连续连续的(否则就应该就做子串)。
给出两个索引i和j,i<j,从A[j..n]中找到最长递增子序列,其中所有元素都比A[i]大。如果用LISbigger(i,j)来表示,使用递归策略得出以下递推式:
如果写出伪代码:
当然这不是完整代码,我们还需要在数组前面插入一个-∞,才能让算法正常执行。至于运行时递推式:$T(n)\leq 2T(n-1)+1,T(n)=O(2^n)$。
最佳二叉查找树
我们最后一个例子结合了递归回溯和分治策略,一次成功的二叉树查找的运行时取决于目标节点的祖先节点数量。作为结果,最坏搜索时间适合二叉树的高度成比例的,二叉树的高度越小越好。
在许多二叉树的应用中,优化所有查找的耗时是优先于单次最坏查找的。如果x是一个比y更加频繁被搜索的目标,我们可以构造一颗x比y的高度更低的树。如果一些节点比另一些节点更受欢迎,一个完全平衡的二叉树并不是最好的选择。事实上,也是一个高度为Ω(n)的完全不平衡的二叉树有可能才是真正最好的选择!
这种情况引申出了接下来的问题。假设给我们一个包含键值A[1..n]的有序数组和它对应的访问频率f[1..n]。我们的目标是构造一个二叉搜索树,使得所有查找时间最少,假设恰好有f[i]次访问价值A[i]。
在我们思考如何解决问题之前,我们应该先提出一个好的递归函数来供我们优化!假设我们有一个节点为$v_1,v_2,…,v_n$的二叉树T,并且排好序了,所以节点$v_i$存储了相应的键值A[i]。接下来忽略常数因子,执行完所有二叉树访问的表达式:
现在假设$v_r$是T的根节点;通过定义,$v_r$是T中所有节点的祖先借点。如果i
第二和第三个求和看起来和我们的原始定义Cost(T,f[1..n])一样。那么做一下简单的置换得到:
那么递推式的边界情况和通常一样,n=0;执行搜索的时间为0。
现在我们任务是计算出可以最小耗时的最佳二叉树$T_{opt}$,假设我们刚好知道$T_{opt}$的根节点是$V_r$。接着由Cost(T,f)的递归定义可知左子树$left(T_{opt})$对于键值数组A[1..r-1]和频率数组f[1..r-1]一定是最佳二叉树。同样的,右子树$right(T_{opt})$对于键值数组A[r+1..n]和频率数组f[r+1..n]一定是最佳二叉树。一旦我们选择了正确的键值存在根节点,通过归纳法可以构造出剩下的最佳二叉树。
如果用OptCost(i,k)表示搜索完f[i..k]次数最佳二叉树的总共耗时,那么这个函数遵循下面这个递推式。
我们的原始问题就是计算OptCost(1,n)。不需要惊讶,这个算法的运行时间又是指数级的。下一章会讲到如何把这个算法优化成多项式级的,所以这里计算确切的运行时没有意义。
分析
又到了算法分析时间,看看这个算法到底有多慢。运行时递推式满足
O(n)符号来自于计算搜索$\sum^{n}_{i=1}f[i]$的所有次数。这个式子看起来确实糟糕,但是前面用过类似的方法来简化这类式子。
现在看起还不错了,直接得出通项公式$T(n)=O(3^n)$。通过这个分析可以看出来我们的递归算法并没有检测所有可能的二叉搜索树!有n个节点的二叉搜索树的数量满足以下递推式
它有一个闭型等式$N(n)=\theta(4^n/\sqrt n)$。我们的算法节约了相当客观的时间通过对每个根节点独立搜索它的左右最佳子树。一个二叉搜索树的全枚举应该考虑所有可能的左右子树;因此得出递推式N(n)。
结语
写完这篇译文后,我感觉自己的翻译速度变快了,而且也比较熟悉作者的推理逻辑了。最后这个小节给我留下了最深刻的印象,所以我几乎是全文翻译的。我个人对运行时计算这块蛮有兴趣的,毕竟这是衡量算法优劣的标准嘛。
原文链接
http://jeffe.cs.illinois.edu/teaching/algorithms/book/02-backtracking.pdf